微分方程第一步吃透概念-复数多项式方程及矩阵理论

  正如我在系列的第一篇文章量子力学之路——坚实的数理基础至关重要，没有捷径可走中提到的那样，学习量子力学有一些，而一些先决条件并不简单，如很多数学主题，这些主题我在“量子力学之路”系列中大多数都会讲到，但不会深入。因此我决定同步开启“

  复数就是形如x+iy的数字，其中x和y是实数，i^2=-1。实数x和y分别称为z的实部和虚部，表示为：

  复数可以绘制在一个矩形网格上，类似于实数对（x，y）被绘制在一个直角坐标系统上。你可以简单地用一对实数(x,y)来确定复数z=x+iy，并绘制（x，y）。y轴称为虚轴，x轴称为实轴。

  系数a_i可能不是实数，但在本系列文章中它们总是实数。在任何情况下，代数基本定理表明，方程p_n(x)=0有n个解。

  但上面的式子是关于x的恒等式，通过令x=r，我们大家可以得到r =0当且仅当p_n(r)=0，也就是说，当且仅当r是p_n(x)的根。

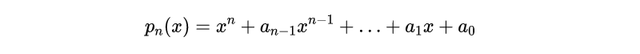
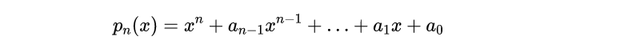
  矩阵是一组数字的矩形数组。一般来说，矩阵用黑体字大写字母表示。我们用A来表示p×q矩阵，它的元素是a_ij。也就是

  只有一列的矩阵称为向量。我们用黑体小写字母来表示向量，这与我们对矩阵的约定一致。A的列向量就是

  行数和列数相同的矩阵称为方阵。方阵的非对角元素是a_ij，其中i≠j。非对角元素都为零的方阵称为对角阵。

  I_n矩阵（其中n是正整数），是所有对角元素都是1的对角矩阵。这些矩阵称为单位矩阵。所以：

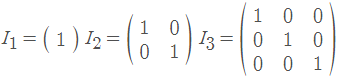
  是单位矩阵。I_n的列被赋予特殊的符号e_1，e_2，…，e_n；也就是：

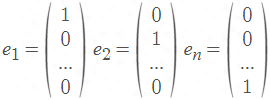
  当上下文明确了I_n的大小时，就可以去掉下标n。那些位于对角线以下的非对角线项为零的方阵称为上三角矩阵（上三角矩阵同理可得）。

  我们定义0矩阵O_n为nXn矩阵，它所有的元素都是0。所以O_n也是对角线。

  我们可以用消元法来解方程组。注意消去过程很大程度上依赖于每个方程中未知变量的系数。

  把方程组的系数和方程组右边的常数放在一起得到一个增广矩阵。化简这个增广矩阵能够获得方程组的解。注意，当系数矩阵简化为单位矩阵时，右边的系数列就是解向量。

  这里的关键点是初等行运算用另一个方程组替换了一个方程组，后者的解集与前者的解集相同。这种解法称为高斯消去法。

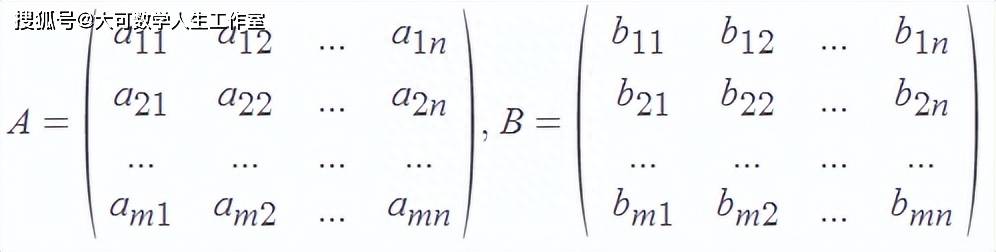
  对于所有的i和j，如果a_ij=b_ij，则A=B。因此，两个矩阵相等，意味着矩阵相应项相等。

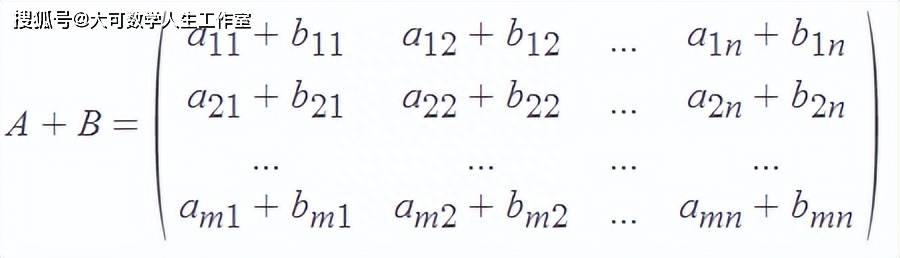
  用第一列替换第一行，用第二列替换第二行，以此类推，直到所有的列都变成行。由这个交换得到的矩阵称为原矩阵的转置，[a_ij]^T=[a_ji]。我们用A^T来表示A的转置。

  一个向量的转置是一个只有一行的矩阵，有时称为行向量。为了尽最大可能避免混淆，我们用逗号分隔行向量的各个元素。

  请注意，转置和加法的定义引出了这样的结论：C=A+B意味着C^T=A^T+B^T。

  如果矩阵A等于它自己的转置，即A^T=A，那么它就是对称的；如果A^T=-A，那么它是反对称的。对称矩阵和反对称矩阵必须是方阵。

  如果A是m×q矩阵，元素为a_ij ；B是q×n矩阵，元素为b_ij，那么乘积C=AB是m×n矩阵，c_ij为：

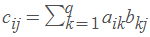
  为了使上面的定义有意义，A的每一行必须有和B的每一列有一样多的元素。这在某种程度上预示着A的列数必须与B的行数相同。

  因此，如果A是2×3矩阵, B是3×3矩阵，那么AB是有定义的，而BA没有定义。因此矩阵乘法是不满足交换律的。

  上面可以写成Ax=b。我们将反复使用这个表达。在不明确A的大小的情况下，我们假设A是m×n，因此x是一个有n个元素的向量，b是一个有m个元素的向量，尽管在大多数应用中m=n。

  为了达到类似的目的，我们引入了矩阵逆的符号。如果存在一个方阵B，使AB=I=BA，那么方阵A就是非奇异的，或者说有一个逆，或是说可逆的。很明显，不是所有的矩阵都有逆矩阵。

  一个不可逆的方阵就是一个A^(-1)不存在的方阵。这样的矩阵称为奇异或不可逆矩阵。

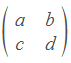
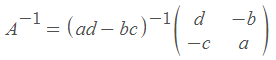
  当且仅当A是奇异阵时，方程组Ax=0有解x≠0。当且仅当A是可逆的，这个方程组只有解x=0。

  A的行列式是一个只在方阵中定义的标量，记作det(A)。它有n的阶乘项，每一项是A的元素的正负乘积：

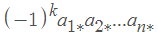
  其中第二个下标，由∗表示，是数字{1，2，…，n}之一，其中没有一个被使用两次。指数k是第二个下标的逆序数。因此，

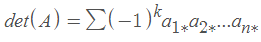
  由于数字{1，2，…，n}的每个排列都有一项，所以上面的和包含n的阶乘项。由于这个原因，实际上并不使用上面的求和来计算。如果n=2，定义是容易使用的，

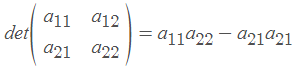
  有两种常用的det(A)的求值方法。在本节中，我们将探讨最高效的方法。该方法依赖于两个基本定理：

  这两个定理为计算行列式提供了一种有效的方法。注意，定理8描述了初等行运算对det(A)的影响。

  我们能够迅速准确地计算初等行变换的结果。所以对于含有已知常数项的矩阵，行化成三角矩阵是计算行列式的首选方法。对于有参数项的矩阵，通常使用其他方法。

  由于矩阵乘法和行列式的定义复杂，乘积的行列式和行列式的乘积之间有着一种简单的关系：

  a_ij的代数余子式写成A_ij，等于余子式乘以 (-1)^(i+j)。代数余子式的重要性是由于以下的重要定理：

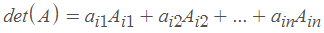
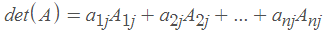
  方程组Ax=0可以有无穷多个解。为了描述这种系统的所有解的集合，我们一定要首先理解线性无关的概念。

  假设已知k个向量a_1， a_2，…，a_k和k个标量c_1 ，c_2…，c_k。考虑到表达式

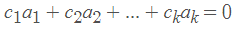
  不是全部为零如果上面的方程对某些标量成立（不是全部为零），那么向量a_1，a_2，…，a_k就是线，…，c_k就叫作权值。由上式可知

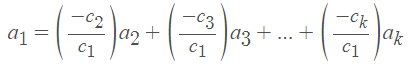
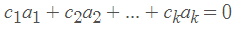
  A，它的列是向量a_1，a_2，…，a_k，它的项的权值是c_1，c_2，…，a_k。因此：

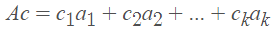
  Ac=0存在非零解时，矩阵A的列向量才是线性无关的。那么，c的元素就是权值。

  A是方阵，那么基于线性相关的行列式的判据是可能和方便的。基本的思想是：如果A是可逆的，那么推论1，系统Ac+0只有平凡解，因为